On the Learning and Learnability of Quasimetrics

Tongzhou Wang
MIT CSAIL
Phillip Isola
MIT CSAIL

ICLR 2022

Paper: [arXiv] [OpenReview]
Code: [GitHub]

Check out our latest works on Quasimetric Learning:
  • Interval Quasimetric Embeddings (IQE)
  • PyTorch Package of SOTA Quasimetric Learning Methods


    • Abstract

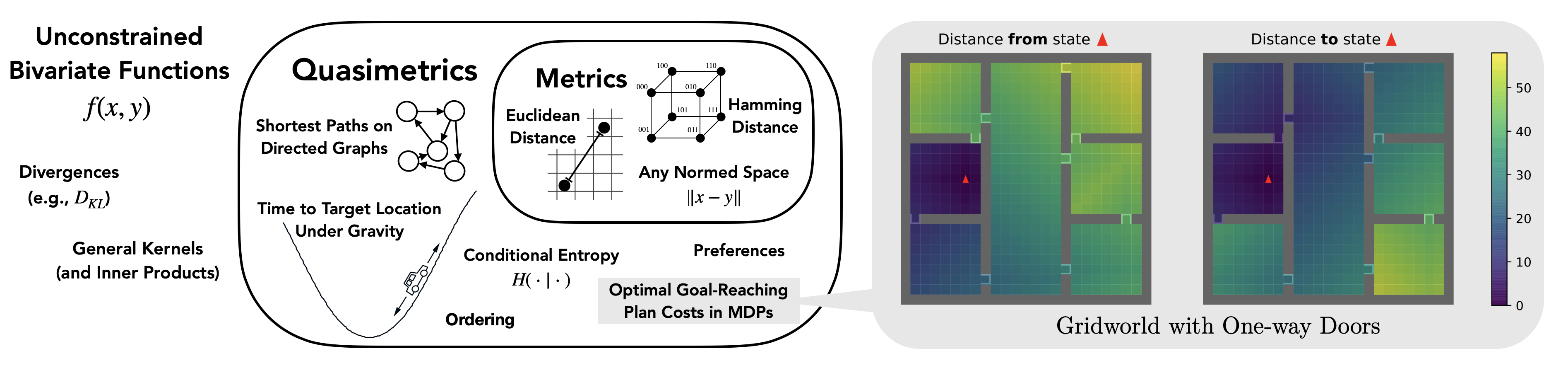
    Our world is full of asymmetries. Gravity and wind can make reaching a place easier than coming back. Social artifacts such as genealogy charts and citation graphs are inherently directed. In reinforcement learning and control, optimal goal-reaching strategies are rarely reversible (symmetrical). Distance functions supported on these asymmetrical structures are called quasimetrics. Despite their common appearance, little research has been done on the learning of quasimetrics.

    Our theoretical analysis reveals that a common class of learning algorithms, including unconstrained multilayer perceptrons (MLPs), provably fails to learn a quasimetric consistent with training data. In contrast, our proposed Poisson Quasimetric Embedding (PQE) is the first quasimetric learning formulation that both is learnable with gradient-based optimization and enjoys strong performance guarantees. Experiments on random graphs, social graphs, and offline Q-learning demonstrate its effectiveness over many common baselines.

    Quasimetric Learning: What and Why?


    Unconstrained bivariate functions is a huge space. A special subset is called quasimetrics, which are similar to metrics but can be asymmetrical. This includes many functions of research interests, which does not generally belong to the widely studied metric function space. Analogous to Metric Learning, we define Quasimetric Learning as the task of learning a quasimetric from data.

    Quasimetric Learning is already an important part of many research works, including graph learning, causual relation learning, and reinforcement learning. Yet understanding and analyses of it are largely missing. Many observations remain unexplained, and there are few principles to guide empirical practices. In this work, we start to fill in this missing piece.

    Three Approaches to Quasimetric Learning


    Existing Approach 1: Search a relaxed hypothesis space for (approximate) quasimetrics

    • E.g., training an unconstrained neural network mapping concatenated input to a scalar output.
    • Common in practice.
    • Theoretical Insight: A large family of methods (including unconstrained networks) fail arbitrarily badly, either failing to fit the training set or far away from being a quasimetric. No (data-agnostic) generalization guarantees can hold.

    Existing Approach 2: Search in an overly restricted hypothesis space that cannot approximate all quasimetrics

    • E.g., training encoders to a latent space with metrics, or quasimetrics restricted to inducing some asymmetric norms.
    • Exists in prior work.
    • Also not proper for general Quasimetric Learning because of their inability to fit arbitrary quasimetrics.

    IDEAL Approach: Search in a space that approximates all quasimetrics and only quasimetrics

    • No known prior work achieves this.
    • Our proposed Poisson Quasimetric Embedding (PQE) is such a method with theoretical guarantees.
    • PQE is a family of differentiable latent-space quasimetrics, usually associated with a jointly trained encoder.
    • One can play with PQEs using our PyTorch package, which includes the initialization and parameterization techniques discussed in the paper.

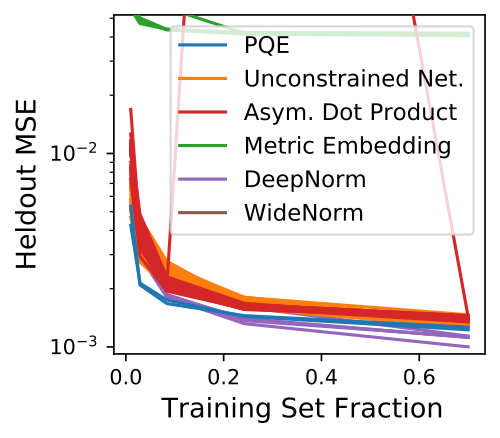
    Empirically, Only PQEs Well Approximate Various Quasimetrics


    Compared Methods:

    • Existing Approach 1: Unconstrained Networks, Dot Products of Asymmetrical Latent Spaces. (Both with possible triangle inequality regularizers)
    • Existing Approach 2: Metric Embddings, DeepNorm, WideNorm.
    • PQEs.

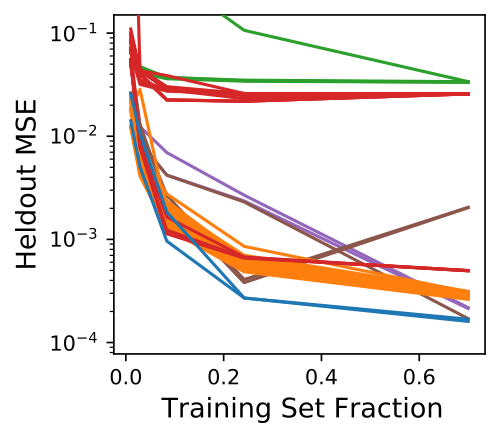
    A Dense Quasimetric

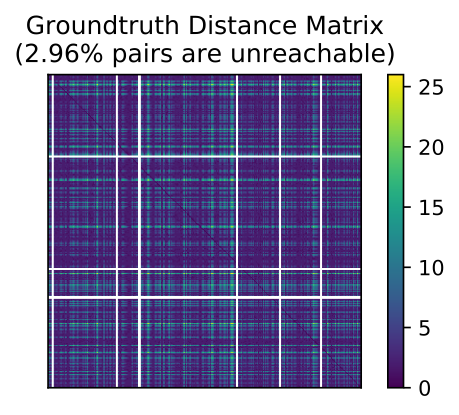
    A Sparse Quasimetric

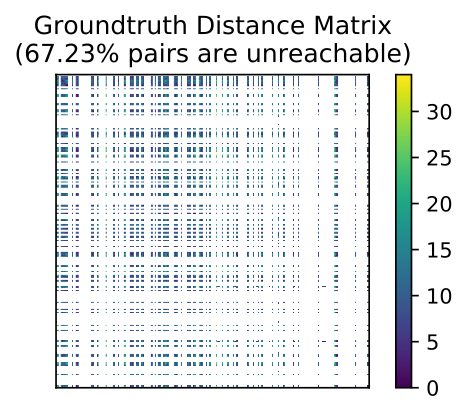
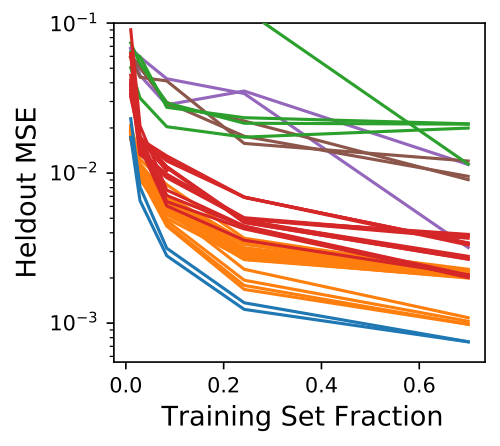
    A Sparse Quasimetric With Block Structure
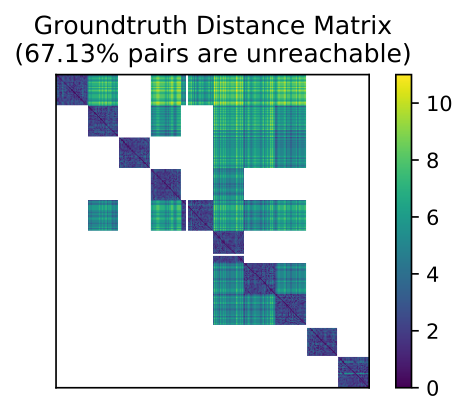
    See the paper for results on large-scale real-life social graphs and on offline Q-learning with a goal-reaching task.
    paper thumbnail

    Paper

    ICLR 2022. arXiv 2206.15478. OpenReview.

    Citation

    Tongzhou Wang, Phillip Isola. "On the Learning and Learnability of Quasimetrics" International Conference on Learning Representations (ICLR). 2022.

    Code: [GitHub]



    bibtex entry

    @inproceedings{tongzhouw2022quasimetrics,
  title={On the Learning and Learnability of Quasimetrics},
  author={Wang, Tongzhou and Isola, Phillip},
  booktitle={International Conference on Learning Representations},
  year={2022}
}