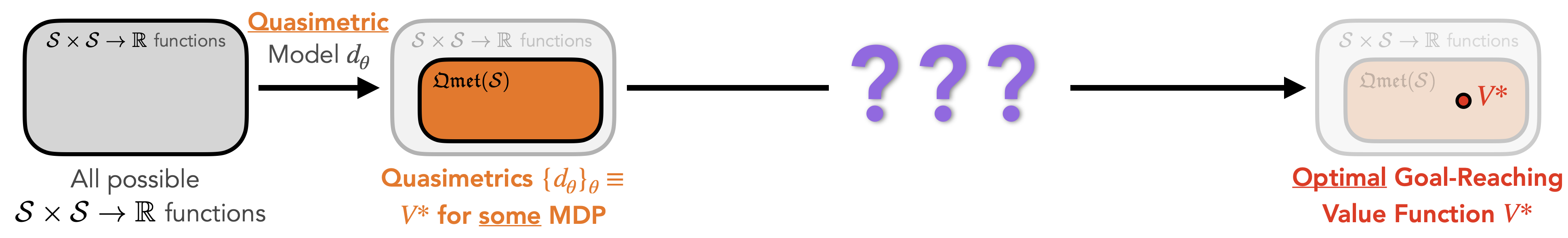| Overview of Quasimetric RL (QRL) |
 Quasimetric Geometry
Quasimetric Geometry
|
+
|
A Novel Objective
(Push apart start state and goal
while maintaining local distances)
|
=
|
Optimal Value $V^*$
AND
High-Performing Goal-Reaching Agents
|
Abstract
In goal-reaching reinforcement learning (RL), the optimal value function has a particular geometry, called quasimetric structure (see also these works). This paper introduces Quasimetric Reinforcement Learning (QRL), a new RL method that utilizes quasimetric models to learn optimal value functions. Distinct from prior approaches, the QRL objective is specifically designed for quasimetrics, and provides strong theoretical recovery guarantees. Empirically, we conduct thorough analyses on a discretized MountainCar environment, identifying properties of QRL and its advantages over alternatives. On offline and online goal-reaching benchmarks, QRL also demonstrates improved sample efficiency and performance, across both state-based and image-based observations.
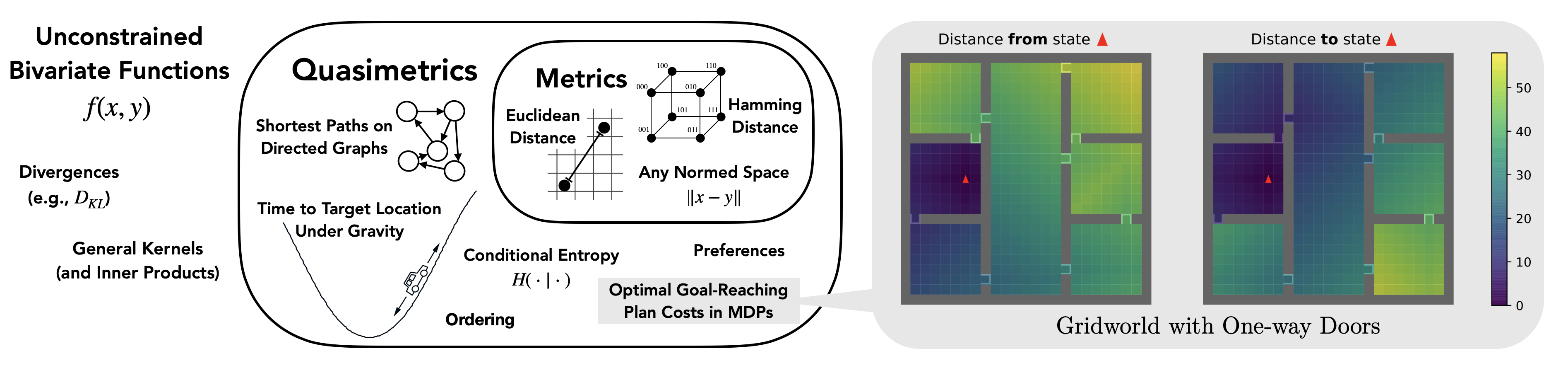
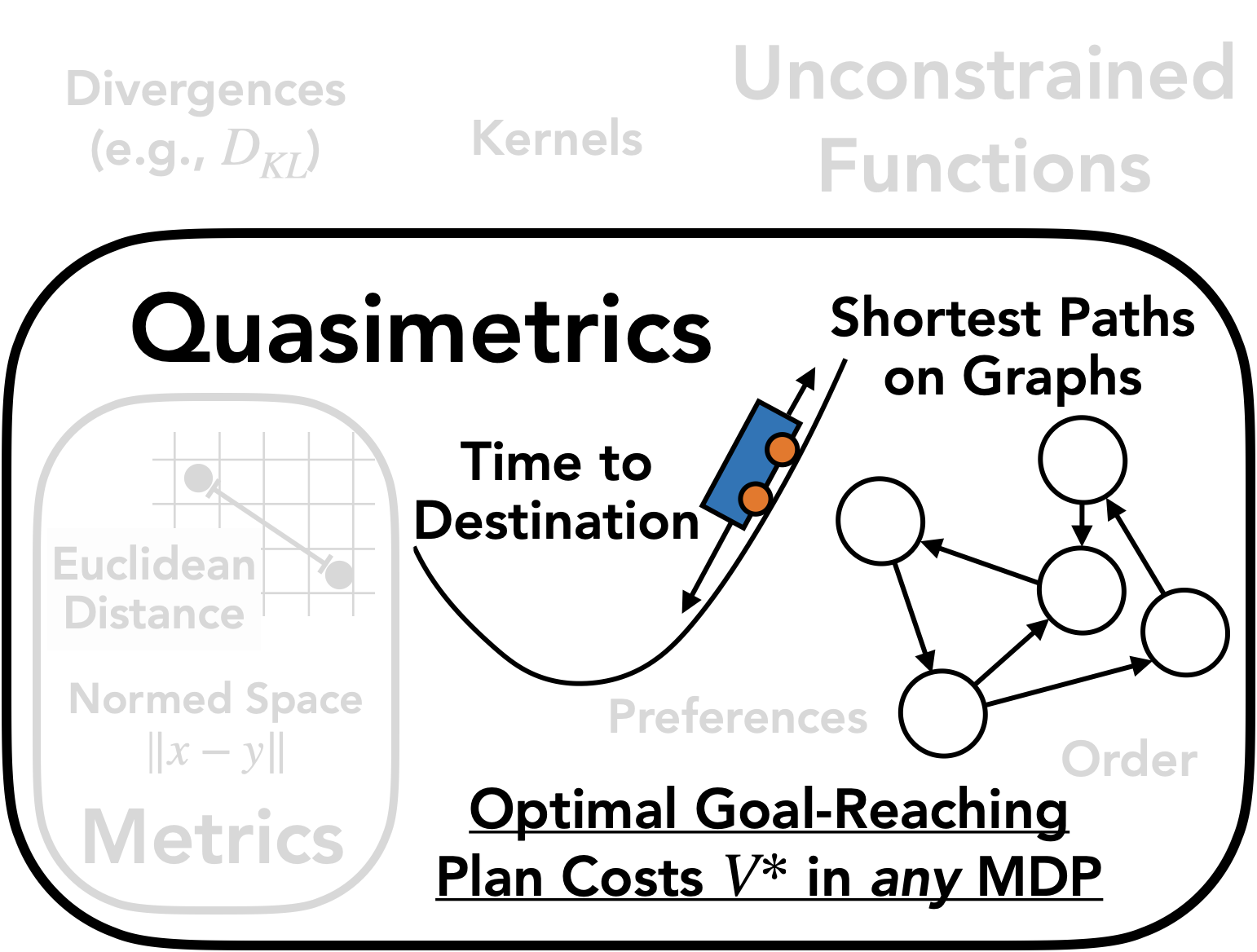
Optimal Value Functions are Quasimetrics
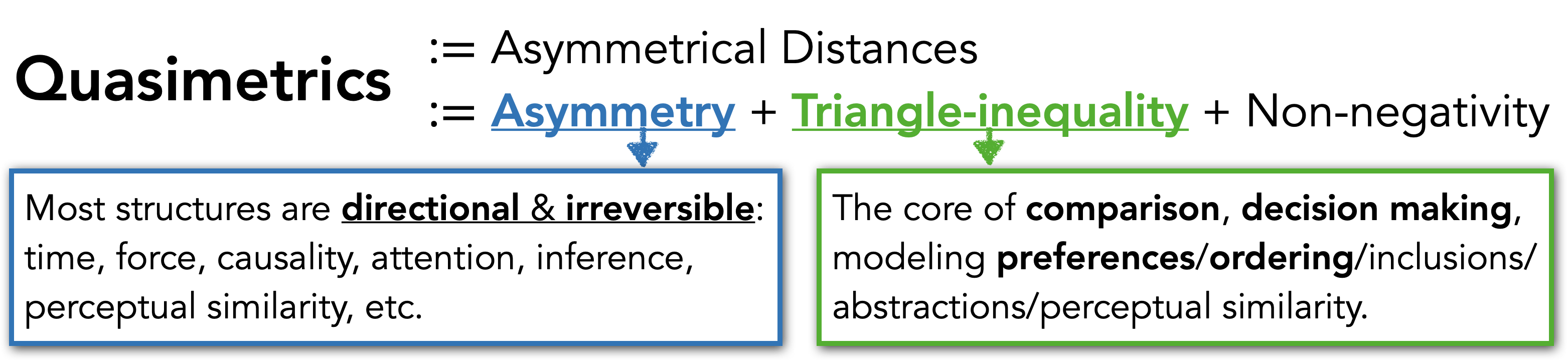
Quasimetrics are a generalization of metrics in that they do not require symmetry. They are well suited for characterizing
optimal cost-to-go (value function) in goal-reaching tasks that generally have
asymmetrical dynamics
E.g., due to time, gravity, actions with irreversible consequences, asymmetrical rules (such as one-way-roads), etc.
and where
triangle-inequality inherently holds.
The optimal path from $A$ to $C$ is at least as good as the optimal path from $A$ to $B$ and then to $C$.
We formalize this in Theorem 1 of our paper, stating that the space of quasimetrics is the exact function class for goal-reaching RL:
$$\textsf{Quasimetrics on state space }\mathcal{S}\equiv\{-V^* \colon V^* \textsf{ is the optimal goal-reaching value of an MDP on }\mathcal{S}\},$$
where $-V^*(s; \textsf{goal}=s_g)$ is the optimal cost-to-go of an MDP from state $s \in \mathcal{S}$ to goal $s_g \in \mathcal{S}$.
Quasimetric Models for Learning Value Functions
Recently proposed
quasimetric models are parametrized models (based on neural networks) $\{d_\theta\}_\theta$ that
$d_\theta$ is a quasimetric (e.g., always satisfying triangle-inequality).
$\{d_\theta\}_\theta$ universally approximates any quasimetric function.
Quasimetric models are thus perfect choices for parametrizing the optimal goal-reaching values $V^*(s; \textsf{goal}=s_g)$ in RL.
One can simply plug such quasimetric models into standard RL algorithms (e.g., Q-learning and DDPG),
as these works do. However, the convergence of such algorithms is
not guaranteed, as
the intermediate results may not be quasimetric functions and cannot be represented by quasimetric models
These algorithms generally rely on policy iteration, temporal-difference learning, or iterative Bellman updates, all of which do converge to optimal $V^*$ with an unconstrained function class, thanks to its capability of representing on-policy values or Bellman update outputs.
However, there is no guarantee that such intermediate results are quasimetrics (see our Theorem 1), and thus the standard convergence results do not directly extend to value functions parametrized by quasimetric models which can only model quasimetrics.
.
Therefore, benefits can be
rather minorE.g., see offline Q-learning results in
these works.
, and sometimes
quasimetric constraints are relaxed.
E.g.,
this work uses quasimetric models in a way that doesn't strictly restrict the value function to be a quasimetric.
Quasimetric Reinforcement Learning (QRL)

|
Our work instead designs a new RL algorithm specifically for quasimetric models, which is called Quasimetric Reinforcement Learning (QRL). In contrast with other RL approaches, QRL directly learns the optimal value function $V^*$ (without policy iteration or temporal-difference learning).
QRL uses a quasimetric model $d_\theta$ to parametrize $-V^*$, restricting search space to quasimetrics that satisfies triangle-inequality
QRL enforces that $d_\theta$ respects the observed local transition costs/distances: $$\forall\ \mathsf{transition}\ (s, a, s', \mathsf{cost}),\quad
{\color{gray}
\underbrace{\color{black}
d_\theta(s; s')
}_{\llap{\mathsf{should\ model\ }-V^*(s; s') = \mathsf{[total}}\rlap{\mathsf{\ cost\ of\ best\ path\ }s \mathsf{\ to\ }s'\mathsf{]}}}
}
\leq
{\color{gray}
\overbrace{\color{black}
\mathsf{cost}
}^{\llap{\mathsf{total\ c}}\rlap{\mathsf{ost\ of\ the\ specific\ path\ }s\ \xrightarrow{\mathsf{action}\ a}\ s'}}
}
\tag{consistent with local costs}$$
Subject to the above constraint, QRL maximally pushes apart the estimated distance/cost between any two states: $$\max_{\theta} \mathbb{E}_{\mathsf{random}\ s_0,s_1} [d_\theta(s_0, s_1)]
\tag{maximize for global costs}$$
In summary, QRL optimizes the following objective:$$
\max_{\theta}~\mathbb{E}_{\substack{s\sim p_\mathsf{state}\\g \sim p_\mathsf{goal}}}[ d_\theta(s, g) ] \qquad \text{subject to }\ \mathbb{E}_{\substack{(s, a, s', \mathsf{cost}) \sim p_\mathsf{transition}}}[ \mathtt{relu}(
{\color{gray}
\underbrace{\color{black}
d_\theta(s, s') - \mathsf{cost}
}_{\llap{\textsf{assume constant cost for}}\rlap{\textsf{ simplicity (can be relaxed)}}}
})^2] \leq
{\color{gray}
\overbrace{\color{black}
\epsilon^2
}^{\llap{\epsilon\textsf{ is a }}\rlap{\textsf{small positive constant}}}
}\tag{QRL}
$$
Why QRL learns optimal $V^*$. Consider two objects connected by multiple chains (video below), where each chain is formed by serveral non-deformable links (i.e., each link is a "local transition" with a fixed length/cost). If we maximally push the two objects apart, the distance will be limited by the shortest of all chains due to the triangle-inequality of our Euclidean physical space. Then, simply measuring the distance between the two objects gives the length of that "optimal" chain connecting them.
Two examples of pushing two pairs of nodes apart. After pushing, the distance (optimal cost) between them can be directly read out.
QRL works exactly in this way, except that it simultaneously pushes apart all pairs in a quasimetric space that can capture the possibly asymmetrical MDP dynamics. Our paper presents rigorous theoretical guarantees that QRL recovers of $V^*$ (Theorems 2 and 3).
See our paper on how to go from this $V^*$ estimate to a $Q^*$ estimate, and then to a policy.
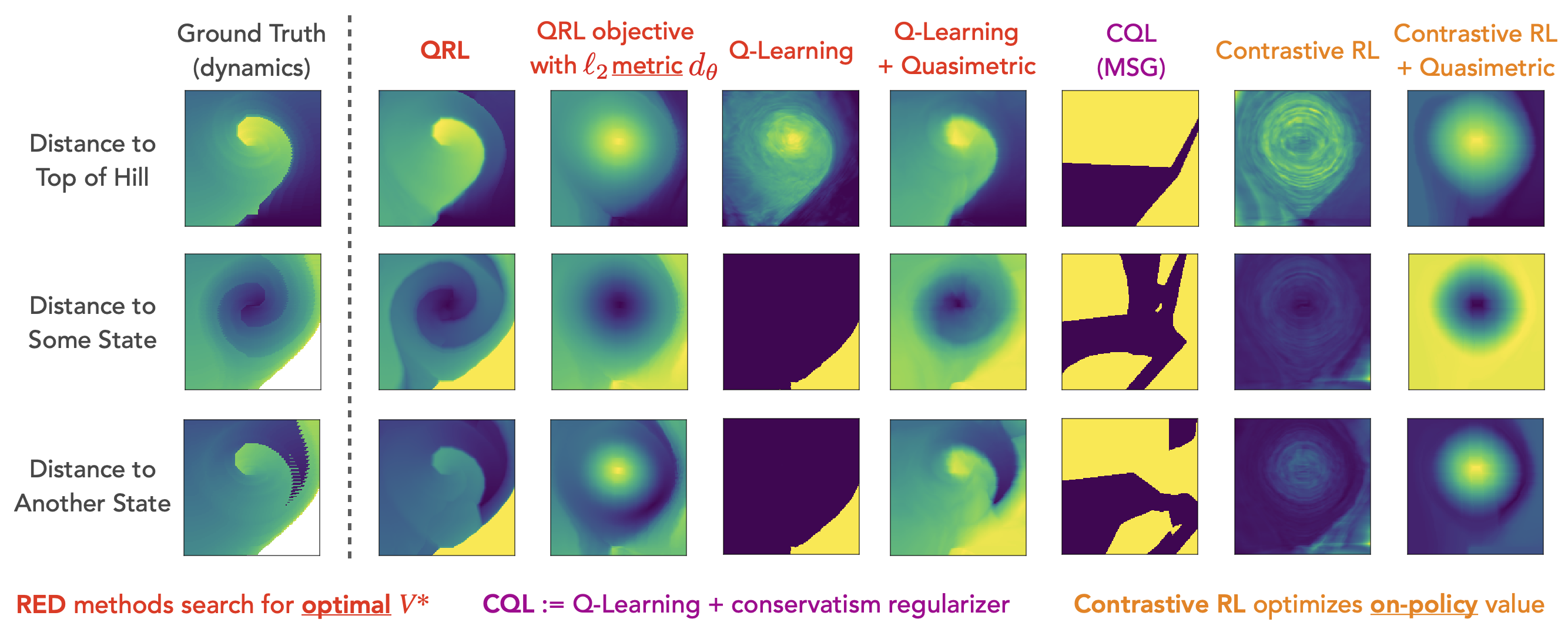
QRL Accurately Recovers $V^*$
Offline Learning on Discretized MountainCar
Visualizations of learned value functions. Only QRL recovers the detailed structure of the ground truth $V^*$ (left section).
Hover for details.
A state in MountainCar is a $2$-dimensional vector containing the car's (horizontal) position and velocity.
Each plot shows the estimated values from every state towards a single goal (indicated in leftmost column) as a 2-dimensional image (velocity as $x$-axis, position as $y$-axis).
Left: Ground truth distances.
Right: Learned value functions from various methods.
Only QRL attains accurately recovers the ground truth distance structure, which crucially relies on the asymmetry of quasimetrics. Q-learning methods generally fail. While their learned values improve with quasimetric models, they still can't capture the fine details. Contrastive RL only inaccurately estimates the on-policy values.
See our paper for control results on this environment.
QRL Quickly Finds High-Quality Policies in Both Offline and Online RL
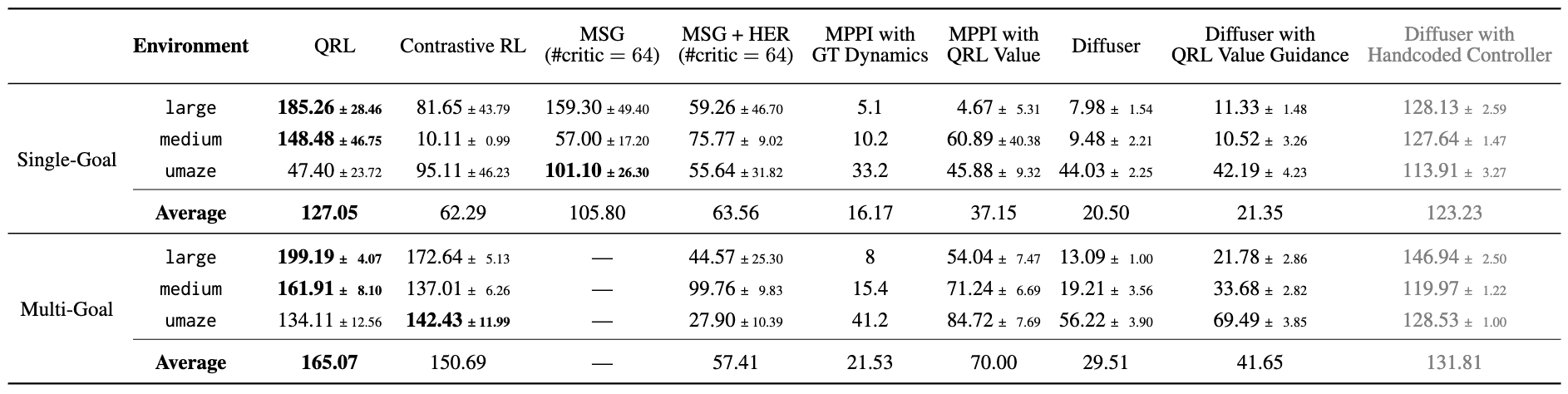
Offline Goal-Reaching maze2d (Normalized Scores/Rewards)
QRL outperforms SOTA offline RL methods, a trajectory modelling method, and Contrastive RL. QRL's learned $V^*$ estimate can be directly used to improve planning (MPPI) and trajectory sampling (Diffuser guided sampling).
Online Goal-Conditional RL Benchmarks with State-based and Image-based Observations
QRL outperforms simply using quasimetric models (MRN or IQE) in DDPG, suggesting the effectiveness of the QRL objective.

|
Paper
ICML 2023. arXiv 2304.01203.
Citation
Tongzhou Wang, Antonio Torralba, Phillip Isola, Amy Zhang. "Optimal Goal-Reaching Reinforcement Learning via Quasimetric Learning"
International Conference on Machine Learning (ICML). 2023.
|
bibtex entry
@inproceedings{tongzhouw2023qrl,
title={Optimal Goal-Reaching Reinforcement Learning via Quasimetric Learning},
author={Wang, Tongzhou and Torralba, Antonio and Isola, Phillip and Zhang, Amy},
booktitle={International Conference on Machine Learning},
organization={PMLR},
year={2023}
}
 Quasimetric Geometry
Quasimetric Geometry
 [arXiv]
[arXiv]